The number of possible features may sometimes be very large and due to the computational complexity it may be necessear to restrict the data to be used. Furthermore, when two features, which contain useful information when treated separately, are combined, the achieved gain may be smaller than expected due to the high mutual correlation. The selection of useful features is extremely important in order to achieve good classification performance. In general, one should aim to use features leading to large between-class distance and small within-class variance.

OUTLIER REMOVAL

According to a definition, an outlier is a point that lies very far (usually a number of times the standard deviation) from the mean of the corresponding random variable. deviation. In a case of normally distributed random variable distances of two and three times the standard deviation cover 95% and 99% of the points, respectively. The problem of outliers is that they produce large error values during the training phase. Thus, they may have crucial effect on the performance of the trained classifier. If the number of outliers is small, a common way is to discard outliers. In general, the long tails of distribution can not be discarded completely. In those cases, a good way is to design a classifier using a cost function which is not so sensitive to these more or less problematic data points.

EXAMPLE OF OUTLIERS

DATA NORMALIZATION

In practice, the values of different features lie within different dynamic ranges, which may cause that features with large values have too significant effect on the cost function when compared to the effect caused by the values in the smaller range. The problem can be solved by using data normalization, after which the feature values lie in the similar range. For N available data of the kth feature one has the following mean and variance, based on which the final normalized value is estimated.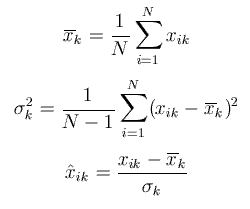

MISSING DATA

The number of available data may not be exactly the same for all the features. In those cases one may either discard some of those features or try to predict them for example by replacing the missing values by mean or interpolated values.