Let us have two classes, w1 and w2, in which the pattern in question belongs and for which the
a priori probabilities P(w1) and P(w2) are known. Furthermore, the class-conditional
probability density functions p(x|wi), i=1,...,M which define the distribution of feature vectors in
each class are assumed to be known. Based on this information the conditional probabilities can be
calculated as follows
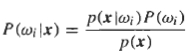
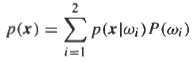
The Bayes classification rule can thus be stated as:
IF P(w2|x)>P(w1|x), x is classified to w2
In the case of equality the pattern can be assigned to either of the classes. An example of two regions, R1 and R2 for the cases of two equiprobable (P(w1)=P(w2)) and classes is shown in the figure below. The variation of p(x|wi), i=1,2, is shown as a function of x. The x0 is a threshold which divides the space into two regions. According to the Bayes decision rule, the x is classified to w1 for all those values of x in R1.
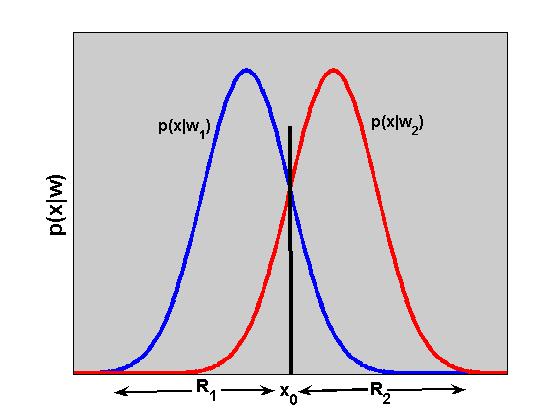
The decision errors are found in the area in which both p(x|w1) and p(x|w2) differ from zero. The error probability Pe can be calculated as follows,

The Bayesian classifier minimizes the classification error probability. However, the classification error probability may not always be the optimal criterion to be adopted for minimization. In some cases some errors may have more serious effects than the others. In those cases the use of a penalty term to weigh each error should be considered.
 Bayes Decision Theory
Bayes Decision Theory