LINEAR CLASSIFIERS

Linear classifiers can be used in cases where classes can be separated by using linear discriminent functions. Two linearly separable classes w1 and w2 are shown in 2-dimensional space in the image below.

In n-dimensional feature space the respective decision hyperplane is stated as

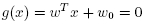
in which w=[w1,...,wn]^T is known as weight vector, w0 is a threshold and T denotes transpose. The following statement

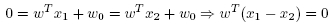
is valid for two data points x1 and x2 which are placed into the hyperplane.

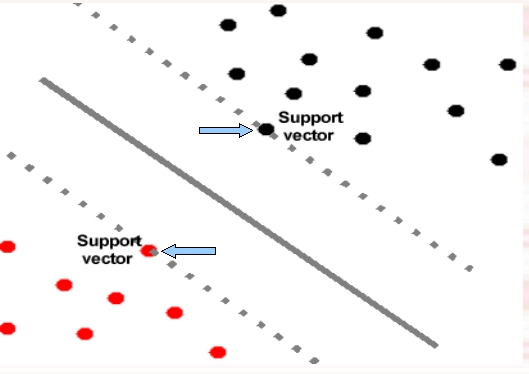
SUPPORT VECTORS

Support vector Machine classifies data by finding a hyperplane which optimally separates the data into two classes. An examole of support vectors is shown below.

NONLINEAR CLASSIFIERS

In the case of nonlinearly separable classes the use of linear classifiers results classification errors, as may seen in the image below.

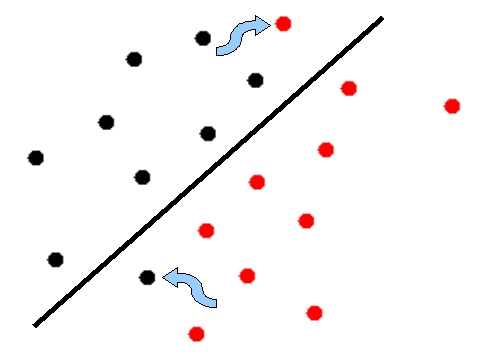
THE XOR PROBLEM

The Exclusive OR (XOR) Boolean function is a typical example of a nonlinearly separable problem. Depending on the input binary values, the output is either 1 or 0, and the data point is classified into class A(1) or B(0). The truth table and the positions of data points (x1,x2) for the XOR problem are given below. It is obvious that classes can not be separated by using one straight line.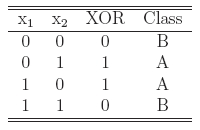

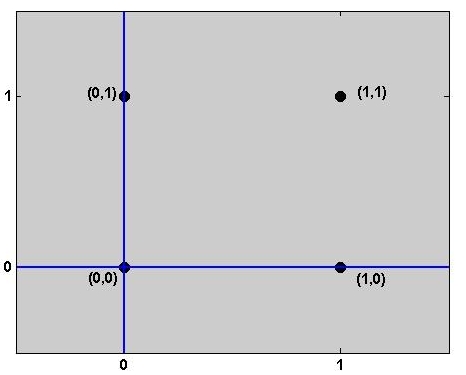
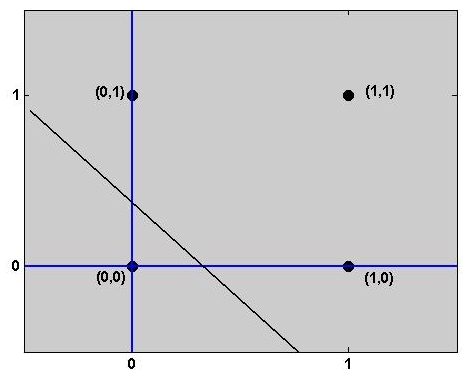
Instead, two other Boolean functions, AND and OR are linearly separable. The truth tables and the positions of data points (x1,x2) for the AND and OR operations are shown below with two possible lines which separate the classes A and B.

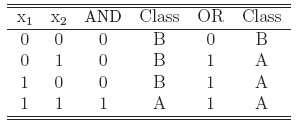
AND (left) - OR (right)

TWO-LAYER PERCEPTRON

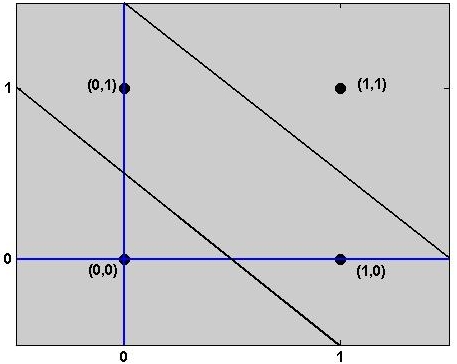
In the case of XOR operation the to classes A and B can be separated by using two straight lines instead of one. Two possible lines, g_1(x) and g_2(x), are shown in the figure below. These lines separate the classes as follows: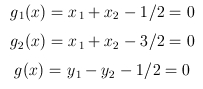

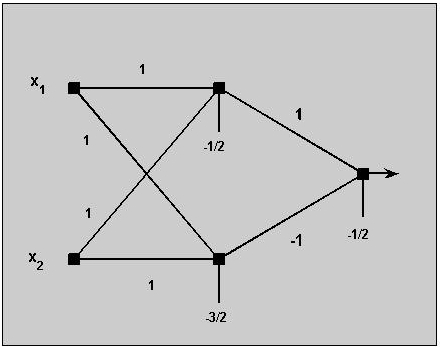
The problem can be solved in two phases. The position of a feature vector x is calculated with respect to the each decision line in the first phase. The results of the first phase are combined in the second phase and the position of x with respect to both lines is found. The truth table for the both phases and the perceptron solving the problem are shown below.

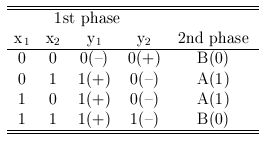
XOR

Perceptron solving the XOR-problem

The polyhedra formed by the neurons of the first hidden layer of a multilayer perceptron is shown below.